
 Next
Next
The column means test is performed separately for each relevant pair of columns within a row that contains mean values and so the formula is presented in terms of one row and one pair of columns.
The following table shows the notation used in this topic.
| Notation | Description |
|---|---|
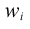 | Weighted count of cases contributing to the mean in column i. |
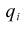 | Sum of squared weights for column i. |
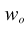 | Weighted count of cases contributing to the mean for the overlap. |
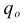 | Sum of squared weights for the overlap. |
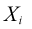 | Weighted sum of the values in column i. |
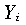 | Weighted sum of the squared values in column i. |
The mean in each column i is
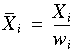
If the effective base is being used, the effective base in each column i is
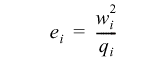
Otherwise
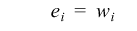
The test is not performed if:
• w i <= 0
• The effective base is being used and q i <= 0
• The mean values in the two columns being tested are identical
The sample variance in column i is
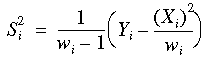
If we set
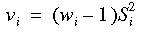
Then the pooled estimate of the population variance is
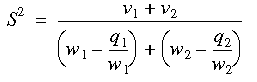
The t value is
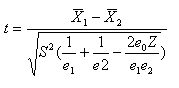
With no overlap, Z and e o are both zero. With overlap, Z is 1.0, except in the case of grids, where it is:
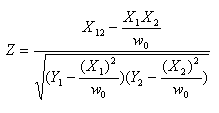
where:
• X12 is the weighted sum, for respondents in both columns, of the value in column 1 multiplied by the value in column 2
• all X and Y terms in Z refer to respondents who are in both columns.
The degrees of freedom, DF, are
DF = e1 + e2 - e0 - 2
Note: The grid overlap formula is applied when the columns have respondents in common, but some (or all) appear in different rows. The grid table normally complies with the rule that there is at least a multiple response categorical variable, or a grid or loop iterator, on both the side and the top.