
 Next
Next
The following table shows the formulae used for conducting the net difference test in IBM® SPSS® Data Collection Survey Reporter.
For any row, and any of the four columns being tested (i=1,2,3, and 4):
| Notation | Description |
|---|---|
| Wi | Sum of the weights (weighted base) for column i. |
| Qi | Sum of the squared weights for column i. |
| Ei = (Wi * Wi) / Qi | Effective base for column i. |
| Pi | Proportion in column i |
For a table with overlap or a grid table, and any pair of columns from the four being tested (i and j=1,2,3, and 4):
| Notation | Description |
|---|---|
| Wij | Sum of the weights (weighted base) for respondents in both columns. |
| Qij | Sum of the squared weights for respondents in both columns. |
| Eij = (Wij * Wij) / Qij | Effective base for respondents in both columns. |
| Pij | Proportion for respondents belonging in the row being tested for both columns. |
The formula is:
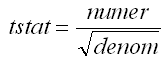
where
numer = (P3 - P4) - (P1 - P2)
and for a non-grid, non-overlap table
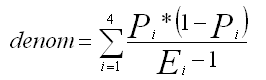
For a table with overlap or a grid table
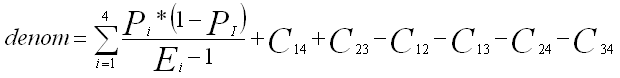
where
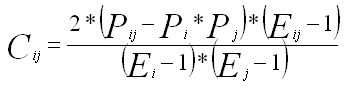
The degrees of freedom are:
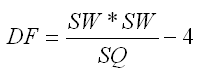
where, for a non-grid, non-overlap table
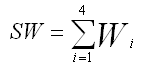
and
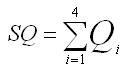
For a table with overlap or a grid table
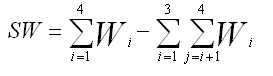
and
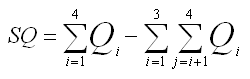
For any row, and any of the four columns being tested (i=1,2,3, and 4):
| Notation | Description |
|---|---|
| Wi | Sum of the weights (weighted base) for column i. |
| Qi | Sum of the squared weights for column i. |
| Ei = (Wi * Wi) / Qi | Effective base for column i. |
| Xi | sum of values for column i |
| Yi | sum of squared values for column i |
| Mi | mean for column i=Xi/Wi |
The values may be either numeric values or factor values.
For a table with overlap or a grid table, and any pair of columns from the four being tested (i and j=1,2,3, and 4):
| Notation | Description |
|---|---|
| Wij | Sum of the weights (weighted base) for respondents in both columns. |
| Qij | Sum of the squared weights for respondents in both columns. |
| Eij = (Wij * Wij) / Qij | Effective base for respondents in both columns. |
The intermediate term SX is:
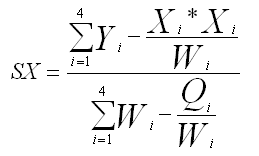
The tstat is
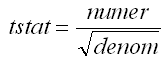
where
numer = (M3 - M4) - (M1 - M2)
and for a grid, non-overlap table,
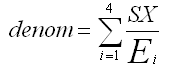
For a table with overlap or a grid table
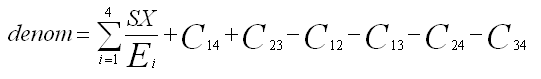
where
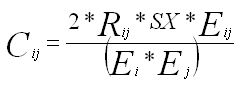
For a non-grid table with overlap, Rij reduces to 1.
For a grid table, it is not possible to display the net difference if the mean is a numeric mean rather than a factor mean. In this case, an error is returned.
For a grid table with factor means:
| Notation | Description |
|---|---|
| Xi* | The weighted sum of factors for column i for all respondents belonging in the mean for column i and in the base of column j. |
| X*j | The weighted sum of factors for column j for all respondents belonging in the mean for column j and in the base of column i. |
| Yi* | The weighted sum of squared factors for column i for all respondents belonging in the mean for column i and in the base of column j |
| Y*j | The weighted sum of squared factors for column j for all respondents belonging in the mean for column j and in the base of column i |
| Yij | The weighted sum of (factor for column i) * (factor for column j) for all respondents belonging in the mean for both columns. |
Using the above terms
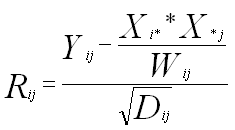
where
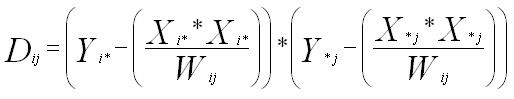
Degrees of freedom
The degrees of freedom are:
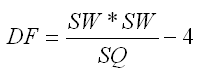
where, for a non-grid, non-overlap table:
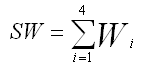
and
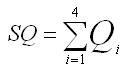
For a table with overlap or a grid table:
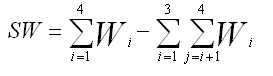
and
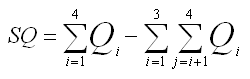
For more on the theory of overlapping samples, see Kish, L (1965), Survey Sampling, New York: John Wiley and Sons. ISBN 0-471-48900-X.