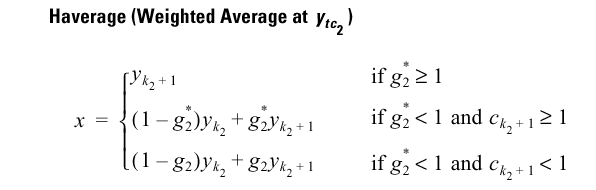Next
Next
This topic provides the formulae used by IBM® SPSS® Data Collection Survey Reporter to calculate the various types of cell contents. The topic is divided into two subsections. The first provides the formulae used to calculate the cell contents that are not dependent on a numeric variable and the second provides the formulae for the summary statistics of numeric variables.
Notation
The following table shows the notation used in this topic except where stated otherwise.
| Notation | Description |
|---|---|
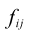 | Sum of cell weights for cases in cell (i, j). |
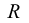 | Number of rows contributing to the test |
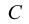 | Number of columns contributing to the test |
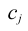 | The jth column subtotal:
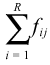 |
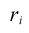 | The ith row subtotal:
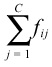 |
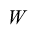 | The grand total: 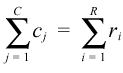 |
The following table provides the formulae used by Survey Reporter to calculate the cell contents that are not dependent on a numeric variable.
| Item | Formula |
|---|---|
| Count |
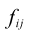 |
| Column Percentage |
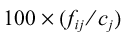 |
| Row Percentage |
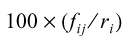 |
| Total Percentage |
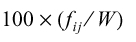 |
| Indice |
 |
| Expected Count |
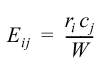 |
| Residual |
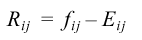 |
Notation
The following table shows additional notation used in the remainder of this topic except where stated otherwise.
| Notation | Description |
|---|---|
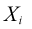 | Value of the variable for case i. |
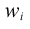 | Weight for case i |
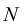 | Number of cases |
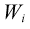 | Sum of the weights for the first i cases |
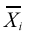 | Mean for the first i cases |
The following table provides the formulae used by Survey Reporter to calculate the cell contents that are dependent on a numeric variable, with the exception of percentiles, the formula for which is shown below the table.
| Item | Formula |
|---|---|
| Mean |
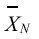 |
| Sum |
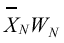 |
| Minimum |
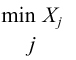 |
| Maximum |
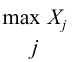 |
| Range |
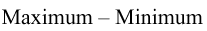 |
| Mode | Value of Xj that has the largest observed frequency. If there are several modes, the first one encountered in the data is selected. |
| Median | The median is the 50th percentile. See Percentile, which is shown below. |
| Variance |
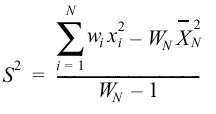 |
| Standard Deviation |
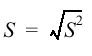 |
| Standard Error |
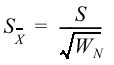 |
Percentile
Survey Reporter uses one method for computation of percentiles. Let
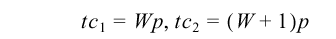
where p is the requested percentile divided by 100, and k1 and k2 satisfy
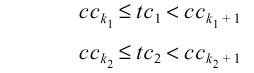
Then
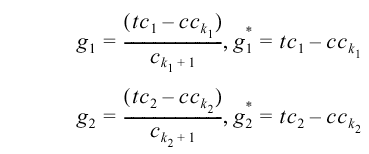
Let x be the pth percentile; the definition is as follows: